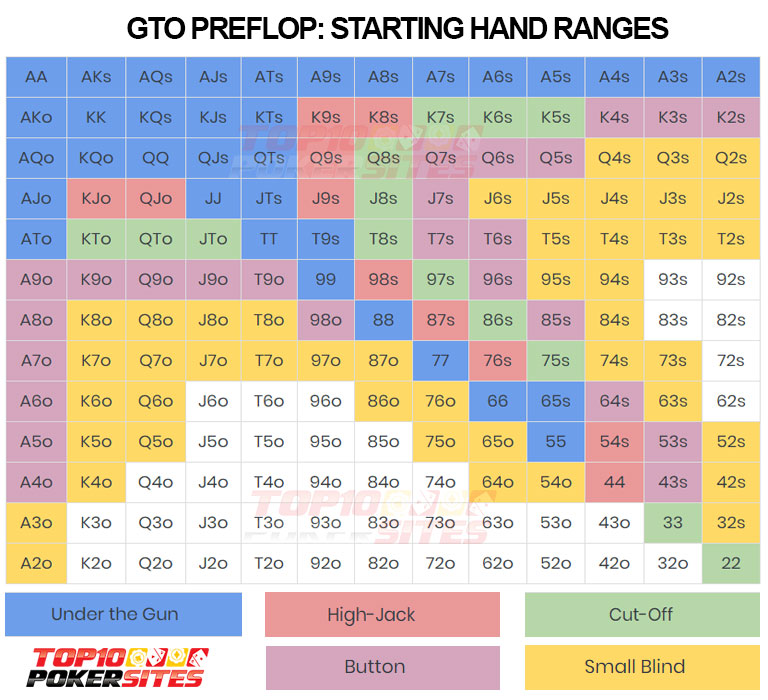
Perfect Poker Strategy
Playing perfect video poker strategy is about understanding the particular variation of video poker you are playing, understanding the video poker PAYTABLE associated with that game, and practice! How to Become a Winning Video Poker Player STEP 1 - PRACTICE Video Poker with our Video Poker Teacher. Keep in mind that the strategy chart on this page was specifically designed for full pay Bonus Deuces. However, many live and online casinos choose to offer less than full pay games, and if that is the case this strategy will be slightly off. It will still be very good, but might not be perfect. Our poker strategy articles cover a diverse range of topics and poker-related issues, including advice for new players, tips for tournament and cash play, introductions to online gambling wallets.
In game theory, trembling hand perfect equilibrium is a refinement of Nash equilibrium due to Reinhard Selten. A trembling hand perfect equilibrium is an equilibrium that takes the possibility of off-the-equilibrium play into account by assuming that the players, through a 'slip of the hand' or tremble, may choose unintended strategies, albeit with negligible probability. And since this poker course is so new, and constantly being updated, it includes some of the very best Zoom poker strategy advice for today's games in my opinion. You will learn the advanced math, game theory, solver theory and exploitative strategy to consistently beat good players in Zoom poker games.
| Subgame Perfect Equilibrium | |
|---|---|
| A solution concept in game theory | |
| Relationship | |
| Subset of | Nash equilibrium |
| Intersects with | Evolutionarily stable strategy |
| Significance | |
| Proposed by | Reinhard Selten |
| Used for | Extensive form games |
| Example | Ultimatum game |
In game theory, a subgame perfect equilibrium (or subgame perfect Nash equilibrium) is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. Every finite extensive game with perfect recall has a subgame perfect equilibrium.[1] Perfect recall is a term introduced by Harold W. Kuhn in 1953 and 'equivalent to the assertion that each player is allowed by the rules of the game to remember everything he knew at previous moves and all of his choices at those moves'.[2]
A common method for determining subgame perfect equilibria in the case of a finite game is backward induction. Here one first considers the last actions of the game and determines which actions the final mover should take in each possible circumstance to maximize his/her utility. One then supposes that the last actor will do these actions, and considers the second to last actions, again choosing those that maximize that actor's utility. This process continues until one reaches the first move of the game. The strategies which remain are the set of all subgame perfect equilibria for finite-horizon extensive games of perfect information.[1] However, backward induction cannot be applied to games of imperfect or incomplete information because this entails cutting through non-singleton information sets.
A subgame perfect equilibrium necessarily satisfies the one-shot deviation principle.
The set of subgame perfect equilibria for a given game is always a subset of the set of Nash equilibria for that game. In some cases the sets can be identical.
The ultimatum game provides an intuitive example of a game with fewer subgame perfect equilibria than Nash equilibria.
Example[edit]
Determining the subgame perfect equilibrium by using backward induction is shown below in Figure 1. Strategies for Player 1 are given by {Up, Uq, Dp, Dq}, whereas Player 2 has the strategies among {TL, TR, BL, BR}. There are 4 subgames in this example, with 3 proper subgames.
Using the backward induction, the players will take the following actions for each subgame:
- Subgame for actions p and q: Player 1 will take action p with payoff (3, 3) to maximize Player 1's payoff, so the payoff for action L becomes (3,3).
- Subgame for actions L and R: Player 2 will take action L for 3 > 2, so the payoff for action D becomes (3, 3).
- Subgame for actions T and B: Player 2 will take action T to maximize Player 2's payoff, so the payoff for action U becomes (1, 4).
- Subgame for actions U and D: Player 1 will take action D to maximize Player 1's payoff.
Thus, the subgame perfect equilibrium is {Dp, TL} with the payoff (3, 3).
An extensive-form game with incomplete information is presented below in Figure 2. Note that the node for Player 1 with actions A and B, and all succeeding actions is a subgame. Player 2's nodes are not a subgame as they are part of the same information set.
The first normal-form game is the normal form representation of the whole extensive-form game. Based on the provided information, (UA, X), (DA, Y), and (DB, Y) are all Nash equilibria for the entire game.

The second normal-form game is the normal form representation of the subgame starting from Player 1's second node with actions A and B. For the second normal-form game, the Nash equilibrium of the subgame is (A, X).
For the entire game Nash equilibria (DA, Y) and (DB, Y) are not subgame perfect equilibria because the move of Player 2 does not constitute a Nash Equilibrium. The Nash equilibrium (UA, X) is subgame perfect because it incorporates the subgame Nash equilibrium (A, X) as part of its strategy.[3]
To solve this game, first find the Nash Equilibria by mutual best response of Subgame 1. Then use backwards induction and plug in (A,X) → (3,4) so that (3,4) become the payoffs for Subgame 2.[3]
The dashed line indicates that player 2 does not know whether player 1 will play A or B in a simultaneous game.

Player 1 chooses U rather than D because 3 > 2 for Player 1's payoff. The resulting equilibrium is (A, X) → (3,4).
Thus, the subgame perfect equilibrium through backwards induction is (UA, X) with the payoff (3, 4).
In finitely repeated games[edit]
For finitely repeated games, if a stage game has only one unique Nash equilibrium, the subgame perfect equilibrium is to play without considering past actions, treating the current subgame as a one-shot game. An example of this is a finitely repeated Prisoner's dilemma game. The Prisoner's dilemma gets its name from a situation that contains two guilty culprits. When they are interrogated, they have the option to stay quiet or defect. If both culprits stay quiet, they both serve a short sentence. If both defect, they both serve a moderate sentence. If they choose opposite options, then the culprit that defects is free and the culprit who stays quiet serves a long sentence. Ultimately, using backward induction, the last subgame in a finitely repeated Prisoner's dilemma requires players to play the unique Nash equilibrium (both players defecting). Because of this, all games prior to the last subgame will also play the Nash equilibrium to maximize their single-period payoffs.[4]If a stage-game in a finitely repeated game has multiple Nash equilibria, subgame perfect equilibria can be constructed to play non-stage-game Nash equilibrium actions, through a 'carrot and stick' structure. One player can use the one stage-game Nash equilibrium to incentivize playing the non-Nash equilibrium action, while using a stage-game Nash equilibrium with lower payoff to the other player if they choose to defect.[5]
Finding subgame-perfect equilibria[edit]
Reinhard Selten proved that any game which can be broken into 'sub-games' containing a sub-set of all the available choices in the main game will have a subgame perfect Nash Equilibrium strategy (possibly as a mixed strategy giving non-deterministic sub-game decisions). Subgame perfection is only used with games of complete information. Subgame perfection can be used with extensive form games of complete but imperfect information.
The subgame-perfect Nash equilibrium is normally deduced by 'backward induction' from the various ultimate outcomes of the game, eliminating branches which would involve any player making a move that is not credible (because it is not optimal) from that node. One game in which the backward induction solution is well known is tic-tac-toe, but in theory even Go has such an optimum strategy for all players. The problem of the relationship between subgame perfection and backward induction was settled by Kaminski (2019), who proved that a generalized procedure of backward induction produces all subgame perfect equilibria in games that may have infinite length, infinite actions as each information set, and imperfect information if a condition of final support is satisfied.
The interesting aspect of the word 'credible' in the preceding paragraph is that taken as a whole (disregarding the irreversibility of reaching sub-games) strategies exist which are superior to subgame perfect strategies, but which are not credible in the sense that a threat to carry them out will harm the player making the threat and prevent that combination of strategies. For instance in the game of 'chicken' if one player has the option of ripping the steering wheel from their car they should always take it because it leads to a 'sub game' in which their rational opponent is precluded from doing the same thing (and killing them both). The wheel-ripper will always win the game (making his opponent swerve away), and the opponent's threat to suicidally follow suit is not credible.
See also[edit]
References[edit]
- ^ abOsborne, M. J. (2004). An Introduction to Game Theory. Oxford University Press.
- ^Kuhn, Harold William; Tucker, Albert William. Contributions to the Theory of Games (AM-28), Volume II. Princeton University Press. ISBN978-1-4008-8197-0.
- ^ abJoel., Watson (2013-05-09). Strategy : an introduction to game theory (Third ed.). New York. ISBN9780393918380. OCLC842323069.
- ^'Prisoner's dilemma'. Encyclopædia Britannica. November 8, 2019. Retrieved December 7, 2020.
first1=missinglast1=(help) - ^Takako, Fujiwara-Greve. Non-cooperative game theory. Tokyo. ISBN9784431556442. OCLC911616270.
External links[edit]
- Selten, R. (1965). Spieltheoretische behandlung eines oligopolmodells mit nachfrageträgheit. Zeitschrift für die gesamte Staatswissenschaft/Journal of Institutional and Theoretical Economics, (H. 2), 301-324, 667-689. [in German - part 1, part 2]
- Java applet to find a subgame perfect Nash Equilibrium solution for an extensive form game from gametheory.net.
- Java applet to find a subgame perfect Nash Equilibrium solution for an extensive form game from gametheory.net.
- Kaminski, M.M. Generalized Backward Induction: Justification for a Folk Algorithm. Games 2019, 10, 34.
Video poker is one of the few casino games where the player's input has a major effect on the outcome of the game. Every time you push Deal you receive five new cards and have a total of thirty-two ways to play the hand. To be a successful video poker player, you have to make the best choice out of those thirty-two options as often as possible.
Since computers can mathematically analyze all thirty-two ways to play any given hand, it is possible to figure out the absolutely correct decision for every hand you receive. However, most players don't carry around high powered computers when they are in the casino, so how is this useful?
Well, fortunately for us, some video poker experts have taken it upon themselves to analyze every single hand that can come off the deck, and assemble their findings into easy to read charts that teach players how to play. Below we have strategy charts for the most common video poker games:
Where to Play Video Poker Online
| Rank | Casino | Sign Up Bonus | Visit Site |
|---|---|---|---|
| #1 | 888 Casino | up to $/€/£888 | Play Now! |
| #2 | Spin Palace Casino | up to $/€/£1000 | Play Now! |
| #3 | Bet365 Casino | up to $/€/£200 | Play Now! |
Most of our pages above list just an expert-level strategy chart that will get you to within 0.1% of the maximum payout percentage for the respective game. Some of the pages also list a beginner-level strategy chart that isn't as accurate, but is easier to follow. If you want to play video poker on your PC check out our guide here. Alternatively, you can also have a look at this site's list of ipad video poker app for real money.
How to Use a Video Poker Strategy Chart
The strategy charts on our site are actually very simple to understand, but to a beginner they may be a bit overwhelming at the start. To use a chart you follow these steps:
- Analyze your hand. Make sure you look at all five of your cards before looking at the chart.
- Start at the top of the chart and work down. You are looking for any spots on the chart where your hand matches up. For example, if you had four hearts in your hand as well as a pair of Kings, it would match up with 'Four to a Flush' as well as 'High Pair'.
- Once you find a couple matches for your hand, observe which one is highest on the chart. Hold the cards indicated by the highest match.
If you still are a little confused, check out the below example to clear things up:
An Example Hand Analysis
Video Poker Perfect Strategy
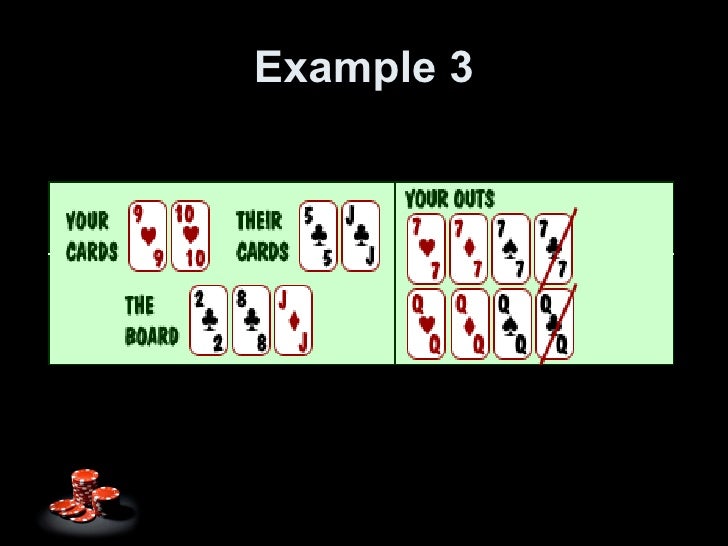
Imagine you are playing a normal Deuces Wild video poker machine. You push 'Draw', and are dealt the hand below:
Ok, so what do we have here as far as options? Well, first of all, we have a Pat Straight, Seven to Jack - a made hand. We also have four clubs, so we have Four to a Flush. If we look at the chart below (a condensed strategy chart for Deuces Wild), we can see that a Pat Straight is just above Four to a Flush, so the Pat Straight is the better hand of the two.
| Hand | Expected Return | Example |
| Pat Royal Flush | 800.0000 | Th-Jh-Qh-Kh-Ah |
| Royal Flush Draw | 19.5957 | Th-Jh-Qh-Kh-4h |
| Pat Straight Flush | 10.0000 | 6h-7h-8h-9h-Th |
| Four of a Kind | 6.2128 | Ac-Ad-As-Ah-5c |
| Pat Full House | 4.0000 | Ac-Ad-As-Js-Jc |
| Pat Flush | 3.0000 | Ac-Jc-6c-5c-4c |
| Three of a Kind | 2.0176 | Ac-Ad-As-Js-Tc |
| Four to a Straight Flush | 1.5745 | 4c-5c-6c-7c-Js |
| Three to a Royal | 1.3053 | Ks-Qs-Js-9c-4c |
| Pat Straight | 1.0000 | 4c-5s-6h-7h-8h |
| Four to a Flush | 0.7660 | Ac-Jc-6c-5c-4h |
But wait! Since all we need for a straight flush is the nine of clubs, we also have Four to a Straight Flush. Because Four to a Straight Flush is higher on the chart than both a Pat Straight and Four to a Flush, the correct play here is to hold the four clubs and discard the nine of spades in hopes of hitting the Straight Flush.
See - it really isn't bad at all, as long as you pay attention to all the cards in your hand.
Holdem Poker Strategy
How Accurate are Strategy Charts?
Another intelligent question to ask is how accurate are these charts? If you find a game that returns 100.5%, but your chart has 0.6% error in it, then you are actually only playing at a 99.9% return - also known as a losing gamble.
Well, the charts on our site are on roughly accurate to within 0.1% of perfect play. So, if you find that game that returns 100.5%, you would be actually earning about 100.4% with our charts - not too bad. Not many charts get much closer than 0.1% because they would have to be extremely long and complicated to explain the subtle differences in rare hands.
Video Poker Strategy Software
There are quite a few programs out there than can develop custom strategy charts for all kinds of games with various pay tables. We have reviewed quite a few of these programs, here are links to our reviews: